A 300 Car Travels at 11m/s What Is Its Momentum

9 Linear Momentum and Collisions

9.5 Collisions in Multiple Dimensions

Learning Objectives

By the finish of this section, you lot will be able to:

Express momentum as a two-dimensional vector
Write equations for momentum conservation in component form
Calculate momentum in two dimensions, as a vector quantity

Information technology is far more than common for collisions to occur in two dimensions; that is, the bending between the initial velocity vectors is neither zero nor

$180\text{°}$

. Let's encounter what complications arise from this.

The first idea we need is that momentum is a vector; like all vectors, it can be expressed as a sum of perpendicular components (usually, though not e'er, an x-component and a y-component, and a z-component if necessary). Thus, when nosotros write downward the statement of conservation of momentum for a trouble, our momentum vectors can be, and usually will be, expressed in component form.

The 2d idea we demand comes from the fact that momentum is related to forcefulness:

$\overset{\to }{F}=\frac{d\overset{\to }{p}}{dt}.$

Expressing both the force and the momentum in component class,

${F}_{x}=\frac{d{p}_{x}}{dt},\enspace{F}_{y}=\frac{d{p}_{y}}{dt},\enspace{F}_{z}=\frac{d{p}_{z}}{dt}.$

Call up, these equations are merely Newton'south 2d law, in vector form and in component class. We know that Newton'south second law is truthful in each direction, independently of the others. Information technology follows therefore (via Newton's third law) that conservation of momentum is also true in each direction independently.

These two ideas motivate the solution to two-dimensional problems: We write down the expression for conservation of momentum twice: once in the ten-direction and once in the y-direction.

$\begin{array}{ccc}\hfill {p}_{\text{f},x}& =\hfill & {p}_{\text{1,i},x}+{p}_{\text{2,i},x}\hfill \\ \hfill {p}_{\text{f},y}& =\hfill & {p}_{\text{1,i},y}+{p}_{\text{2,i},y}\hfill \end{array}$

This process is shown graphically in (Figure).

Figure a, titled break initial momentum into x and y components shows vector p 1 i as a solid arrow pointing to the right and down. Its components are shown as dashed arrows: p 1 i y points down from the tail of p 1 i and p 1 i x points to the right from the head of p 1 i y to the head of p 1 i. Vector p 2 i is shown as a solid arrow with its tail at the head of vector p 1 i, and is shorter than p 1 i. Vector p 2 i points to the right and up. Its components are shown as dashed arrows: p 2 i x points to the right from the tail of p 2 i and p 2 i y points up from the head of p 2 i x to the head of p 2 i. Vector p f points from the tail of p 1 i to the head of p 2 i, pointing to the right and slightly down. Figure b titled add x and y components to obtain x and y components of final momentum shows the vector sums of the components. P 1 i y is a downward arrow. P 2 i y is a shorter upward arrow, aligned with its tail at the head of P 1 i y. P f y is a short downward arrow that starts at the tail of P 1 i y and ends at the head of P 2 i y. P 1 i x is a rightward arrow. P 2 i x is a shorter rightward arrow, aligned with its tail at the head of P 1 i x. P f x is a long rightward arrow that starts at the tail of P 1 i x and ends at the head of P 2 i x. Figure c, titled add x and y components of final momentum shows the right triangle formed by sides p f x and p f y and hypotenuse p f. Arrows from figure b indicate that p f x and p f y are the same in figures b and c. — **Figure 9.22** (a) For 2-dimensional momentum problems, intermission the initial momentum vectors into their x- and y-components. (b) Add the x- and y-components together separately. This gives yous the x- and y-components of the final momentum, which are shown equally red dashed vectors. (c) Calculation these components together gives the final momentum.

We solve each of these 2 component equations independently to obtain the 10– and y-components of the desired velocity vector:

$\begin{array}{ccc}\hfill {v}_{\text{f},x}& =\hfill & \frac{{m}_{1}{v}_{\text{1,i},x}+{m}_{2}{v}_{\text{2,i},x}}{m}\hfill \\ \hfill {v}_{\text{f},y}& =\hfill & \frac{{m}_{1}{v}_{\text{1,i},y}+{m}_{2}{v}_{\text{2,i},y}}{m}.\hfill \end{array}$

(Hither, m represents the total mass of the system.) Finally, combine these components using the Pythagorean theorem,

${v}_{\text{f}}=|{\overset{\to }{v}}_{f}|=\sqrt{{v}_{\text{f},x}^{2}+{v}_{\text{f},y}^{2}}.$

Problem-Solving Strategy: Conservation of Momentum in Two Dimensions

The method for solving a two-dimensional (or even iii-dimensional) conservation of momentum problem is by and large the same as the method for solving a i-dimensional trouble, except that yous have to conserve momentum in both (or all three) dimensions simultaneously:

Identify a closed system.
Write downwards the equation that represents conservation of momentum in the x-direction, and solve it for the desired quantity. If you are calculating a vector quantity (velocity, ordinarily), this will give y'all the x-component of the vector.
Write downward the equation that represents conservation of momentum in the y-direction, and solve. This will give you the y-component of your vector quantity.
Assuming you are calculating a vector quantity, apply the Pythagorean theorem to calculate its magnitude, using the results of steps 3 and 4.

Instance

Traffic Standoff

A small car of mass 1200 kg traveling east at 60 km/60 minutes collides at an intersection with a truck of mass 3000 kg that is traveling due due north at xl km/hr ((Figure)). The two vehicles are locked together. What is the velocity of the combined wreckage?

An x y coordinate system is shown. A large truck mass m T = 3000 kilograms is moving north toward the origin with velocity v T. A small car mass m c = 1200 kilograms is moving east toward the origin with velocity v c, which is less than v T. — **Effigy nine.23** A large truck moving north is almost to collide with a small car moving east. The final momentum vector has both x- and y-components.

Strategy

Offset off, we need a closed system. The natural system to choose is the (machine + truck), just this organisation is not closed; friction from the road acts on both vehicles. We avoid this problem by restricting the question to finding the velocity at the instant just after the collision, so that friction has non yet had any effect on the arrangement. With that restriction, momentum is conserved for this system.

Since there are two directions involved, we exercise conservation of momentum twice: once in the x-direction and once in the y-direction.

SolutionBefore the collision the total momentum is

$\overset{\to }{p}={m}_{\text{c}}{\overset{\to }{v}}_{\text{c}}+{m}_{\text{T}}{\overset{\to }{v}}_{\text{T}}.$

Later the collision, the wreckage has momentum

$\overset{\to }{p}=({m}_{\text{c}}+{m}_{\text{T}}){\overset{\to }{v}}_{w}.$

Since the system is closed, momentum must be conserved, so nosotros have

${m}_{\text{c}}{\overset{\to }{v}}_{c}+{m}_{\text{T}}{\overset{\to }{v}}_{\text{T}}=({m}_{\text{c}}+{m}_{\text{T}}){\overset{\to }{v}}_{w}.$

Nosotros have to be conscientious; the two initial momenta are not parallel. We must add together vectorially ((Figure)).

Arrow p c points horizontally to the right. Arrow p t points vertically upward. The head of p t meets the tail of p c. P t is longer than p t. A dashed line is shown from the tail of p t to the head of p c. The angle between the dashed line and p t, at the tail of p t, is labeled as theta. — **Figure 9.24** Graphical addition of momentum vectors. Notice that, although the car'due south velocity is larger than the truck'south, its momentum is smaller.

If we define the +ten-direction to point eastward and the +y-management to signal due north, as in the figure, and so (conveniently),

$\begin{array}{ccc}\hfill {\overset{\to }{p}}_{\text{c}}& =\hfill & {p}_{\text{c}}\hat{i}={m}_{\text{c}}{v}_{\text{c}}\hat{i}\hfill \\ \hfill {\overset{\to }{p}}_{\text{T}}& =\hfill & {p}_{\text{T}}\hat{j}={m}_{\text{T}}{v}_{\text{T}}\hat{j}.\hfill \end{array}$

Therefore, in the x-direction:

$\begin{array}{ccc}\hfill {m}_{\text{c}}{v}_{\text{c}}& =\hfill & ({m}_{\text{c}}+{m}_{\text{T}}){v}_{\text{w},x}\hfill \\ \hfill {v}_{\text{w},x}& =\hfill & (\frac{{m}_{\text{c}}}{{m}_{\text{c}}+{m}_{\text{T}}}){v}_{\text{c}}\hfill \end{array}$

and in the y-direction:

$\begin{array}{ccc}\hfill {m}_{\text{T}}{v}_{\text{T}}& =\hfill & ({m}_{\text{c}}+{m}_{\text{T}}){v}_{\text{w},y}\hfill \\ \hfill {v}_{\text{w},y}& =\hfill & (\frac{{m}_{\text{T}}}{{m}_{\text{c}}+{m}_{\text{T}}}){v}_{\text{T}}.\hfill \end{array}$

Applying the Pythagorean theorem gives

$\begin{array}{cc}\hfill |{\overset{\to }{v}}_{w}|& =\sqrt{{[(\frac{{m}_{\text{c}}}{{m}_{\text{c}}+{m}_{t}}){v}_{\text{c}}]}^{2}+{[(\frac{{m}_{t}}{{m}_{\text{c}}+{m}_{t}}){v}_{t}]}^{2}}\hfill \\ & =\sqrt{{[(\frac{1200\,\text{kg}}{4200\,\text{kg}})(16.67\,\frac{\text{m}}{\text{s}})]}^{2}+{[(\frac{3000\,\text{kg}}{4200\,\text{kg}})(11.1\,\frac{\text{m}}{\text{s}})]}^{2}}\hfill \\ & =\sqrt{{(4.76\,\frac{\text{m}}{\text{s}})}^{2}+{(7.93\,\frac{\text{m}}{\text{s}})}^{2}}\hfill \\ & =9.25\,\frac{\text{m}}{\text{s}}\approx 33.3\,\frac{\text{km}}{\text{hr}}.\hfill \end{array}$

As for its direction, using the angle shown in the figure,

$\theta ={\text{tan}}^{-1}(\frac{{v}_{\text{w},x}}{{v}_{\text{w},y}})={\text{tan}}^{-1}(\frac{7.93\,\text{m/s}}{4.76\,\text{m/s}})=59\text{°}.$

This bending is east of north, or

$31\text{°}$

counterclockwise from the +ten-direction.

Significance

Every bit a practical matter, blow investigators usually piece of work in the "opposite direction"; they measure the distance of skid marks on the road (which gives the stopping distance) and apply the work-free energy theorem along with conservation of momentum to make up one's mind the speeds and directions of the cars prior to the standoff. We saw that analysis in an earlier section.

Check Your Understanding

Suppose the initial velocities were not at correct angles to each other. How would this modify both the physical result and the mathematical analysis of the collision?

[reveal-answer q="fs-id1167133455456″]Show Solution[/reveal-answer]

[hidden-respond a="fs-id1167133455456″]

Were the initial velocities not at correct angles, then one or both of the velocities would take to be expressed in component form. The mathematical analysis of the problem would be slightly more involved, but the physical issue would not change.

[/hidden-answer]

Example

Exploding Scuba Tank

A mutual scuba tank is an aluminum cylinder that weighs 31.7 pounds empty ((Figure)). When full of compressed air, the internal pressure is between 2500 and 3000 psi (pounds per square inch). Suppose such a tank, which had been sitting motionless, suddenly explodes into three pieces. The kickoff piece, weighing 10 pounds, shoots off horizontally at 235 miles per 60 minutes; the second piece (7 pounds) shoots off at 172 miles per 60 minutes, also in the horizontal plane, but at a

$19\text{°}$

angle to the first piece. What is the mass and initial velocity of the tertiary piece? (Do all piece of work, and limited your concluding respond, in SI units.)

A drawing of a scuba tank exploding, and the resulting three pieces of different sizes. — **Figure 9.25** A scuba tank explodes into three pieces.

Strategy

To use conservation of momentum, we need a airtight organization. If we define the arrangement to be the scuba tank, this is not a closed system, since gravity is an external forcefulness. However, the problem asks for the just the initial velocity of the third slice, and then nosotros can fail the issue of gravity and consider the tank past itself as a closed arrangement. Detect that, for this system, the initial momentum vector is zero.

Nosotros choose a coordinate organisation where all the move happens in the xy-plane. Nosotros and then write down the equations for conservation of momentum in each direction, thus obtaining the x– and y-components of the momentum of the third piece, from which we obtain its magnitude (via the Pythagorean theorem) and its management. Finally, dividing this momentum by the mass of the third slice gives us the velocity.

Solution

First, let'south go all the conversions to SI units out of the way:

$\begin{array}{cc} 31.7\,\text{lb}\,×\,\frac{1\text{\hspace{0.17em}}\text{kg}}{2.2\,\text{lb}}\to 14.4\,\text{kg}\hfill \\ 10\,\text{lb}\to 4.5\,\text{kg}\hfill \\ 235\,\frac{\text{miles}}{\text{hour}}\,×\,\frac{1\,\text{hour}}{3600\,\text{s}}\,×\,\frac{1609\,\text{m}}{\text{mile}}=105\,\frac{\text{m}}{\text{s}}\hfill \\ 7\,\text{lb}\to 3.2\,\text{kg}\hfill \\ 172\,\frac{\text{mile}}{\text{hour}}=77\,\frac{\text{m}}{\text{s}}\hfill \\ {m}_{3}=14.4\,\text{kg}-(4.5\,\text{kg}+3.2\,\text{kg})=6.7\,\text{kg.}\hfill \end{array}$

Now apply conservation of momentum in each direction.

The three pieces of the scuba tank are shown on an x y coordinate system. The medium size piece is on the positive x axis and has momentum p 1 in the plus x direction. The smallest piece is at an angle theta above the positive x axis and has momentum p 2. The largest piece is at an angle phi below the negative x axis and has momentum p 3.

x-management:

$\begin{array}{ccc}\hfill {p}_{\text{f,}x}& =\hfill & {p}_{\text{0,}x}\hfill \\ \hfill {p}_{\text{1,}x}+{p}_{\text{2,}x}+{p}_{\text{3,}x}& =\hfill & 0\hfill \\ \hfill {m}_{1}{v}_{\text{1,}x}+{m}_{2}{v}_{\text{2,}x}+{p}_{\text{3,}x}& =\hfill & 0\hfill \\ \hfill {p}_{\text{3,}x}& =\hfill & \text{−}{m}_{1}{v}_{\text{1,}x}-{m}_{2}{v}_{\text{2,}x}\hfill \end{array}$

y-direction:

$\begin{array}{ccc}\hfill {p}_{\text{f,}y}& =\hfill & {p}_{\text{0,}y}\hfill \\ \hfill {p}_{\text{1,}y}+{p}_{\text{2,}y}+{p}_{\text{3,}y}& =\hfill & 0\hfill \\ \hfill {m}_{1}{v}_{\text{1,}y}+{m}_{2}{v}_{\text{2,}y}+{p}_{\text{3,}y}& =\hfill & 0\hfill \\ \hfill {p}_{\text{3,}y}& =\hfill & \text{−}{m}_{1}{v}_{\text{1,}y}-{m}_{2}{v}_{\text{2,}y}\hfill \end{array}$

From our chosen coordinate system, we write the 10-components as

$\begin{array}{cc}\hfill {p}_{3,x}& =\text{−}{m}_{1}{v}_{1}-{m}_{2}{v}_{2}\text{cos}\theta \hfill \\ & =\text{−}(14.5\,\text{kg})(105\,\frac{\text{m}}{\text{s}})-(4.5\,\text{kg})(77\,\frac{\text{m}}{\text{s}})\text{cos}(19\text{°})\hfill \\ & =-1850\frac{\text{kg}·\text{m}}{\text{s}}.\hfill \end{array}$

For the y-direction, we have

$\begin{array}{cc}\hfill {p}_{3y}& =0-{m}_{2}{v}_{2}\text{sin}\theta \hfill \\ & =\text{−}(4.5\,\text{kg})(77\,\frac{\text{m}}{\text{s}})\text{sin}(19\text{°})\hfill \\ & =-113\,\frac{\text{kg}·\text{m}}{\text{s}}.\hfill \end{array}$

This gives the magnitude of

${p}_{3}$

$\begin{array}{cc}\hfill {p}_{3}& =\sqrt{{p}_{\text{3,}x}^{2}+{p}_{\text{3,}y}^{2}}\hfill \\ & =\sqrt{{(-1850\,\frac{\text{kg}·\text{m}}{\text{s}})}^{2}+(-113\,\frac{\text{kg}·\text{m}}{\text{s}})}\hfill \\ & =1854\,\frac{\text{kg}·\text{m}}{\text{s}}.\hfill \end{array}$

The velocity of the 3rd piece is therefore

${v}_{3}=\frac{{p}_{3}}{{m}_{3}}=\frac{1854\,\frac{\text{kg}·\text{m}}{\text{s}}}{6.7\,\text{kg}}=277\,\frac{\text{m}}{\text{s}}.$

The management of its velocity vector is the same as the management of its momentum vector:

$\varphi ={\text{tan}}^{-1}(\frac{{p}_{\text{3,}y}}{{p}_{\text{3,}x}})={\text{tan}}^{-1}(\frac{113\,\frac{\text{kg}·\text{m}}{\text{s}}}{1850\,\frac{\text{kg}·\text{m}}{\text{s}}})=3.5\text{°}.$

Because

$\varphi$

is beneath the

$\text{−}x$

-axis, the actual angle is

$183.5\text{°}$

from the +x-direction.

Significance

The enormous velocities here are typical; an exploding tank of any compressed gas can easily punch through the wall of a house and crusade pregnant injury, or death. Fortunately, such explosions are extremely rare, on a percentage ground.

Check Your Understanding

Discover that the mass of the air in the tank was neglected in the analysis and solution. How would the solution method inverse if the air was included? How large a departure do you think it would make in the final respond?

[reveal-answer q="fs-id1167133523735″]Show Solution[/reveal-answer]

[hidden-reply a="fs-id1167133523735″]

The volume of a scuba tank is virtually 11 L. Assuming air is an ideal gas, the number of gas molecules in the tank is

$\begin{array}{ccc}\hfill PV& =\hfill & NRT\hfill \\ \hfill N& =\hfill & \frac{PV}{RT}=\frac{(2500\,\text{psi})(0.011\,{\text{m}}^{3})}{(8.31\,\text{J/mol}·\text{K})(300\,\text{K})}(\frac{6894.8\,\text{Pa}}{1\,\text{psi}})\hfill \\ & =\hfill & 7.59\,×\,{10}^{1}\,\text{mol}\hfill \end{array}$

The average molecular mass of air is 29 grand/mol, so the mass of air independent in the tank is most 2.2 kg. This is about x times less than the mass of the tank, so it is condom to neglect it. Also, the initial force of the air pressure level is roughly proportional to the surface area of each piece, which is in turn proportional to the mass of each slice (assuming uniform thickness). Thus, the initial dispatch of each slice would change very little if we explicitly consider the air.

[/hidden-answer]

Summary

The approach to ii-dimensional collisions is to choose a user-friendly coordinate system and interruption the motion into components along perpendicular axes.
Momentum is conserved in both directions simultaneously and independently.
The Pythagorean theorem gives the magnitude of the momentum vector using the x– and y-components, calculated using conservation of momentum in each direction.

Conceptual Questions

Momentum for a system tin be conserved in one direction while non existence conserved in some other. What is the angle between the directions? Give an example.

[reveal-answer q="fs-id1167132326318″]Prove Solution[/reveal-reply]

[hidden-reply a="fs-id1167132326318″]

The angle betwixt the directions must be 90°. Whatever arrangement that has nix internet external force in one management and nonzero net external strength in a perpendicular direction volition satisfy these weather condition.

[/hidden-answer]

Problems

A ane.lxxx-kg falcon is diving at 28.0 m/s at a down angle of

$35\text{°}$

. Information technology catches a 0.650-kg dove from behind in midair. What is their combined velocity later bear on if the pigeon's initial velocity was 7.00 1000/s directed horizontally? Note that

${\hat{v}}_{\text{1,}\text{i}}$

is a unit vector pointing in the direction in which the hawk is initially flying.

A hawk is flying toward a dove. The hawk is moving in a direction that is 35 degrees down from the horizontal at v 1 i = 28.0 meters per second v 1 i hat. The dove is moving to the right at 7.00 meters per second i hat.

(credit "hawk": modification of piece of work by "USFWS Mount-Prairie"/Flickr; credit "pigeon": modification of work by Jacob Spinks)

[reveal-reply q="501216″]Prove Answer[/reveal-answer]
[hidden-reply a="501216″]22.i k/s at

$32.2\text{°}$

below the horizontal[/hidden-answer]

A billiard ball, labeled 1, moving horizontally strikes another billiard ball, labeled 2, at rest. Before impact, brawl 1 was moving at a speed of 3.00 m/s, and afterwards impact it is moving at 0.50 thou/s at l° from the original direction. If the ii balls take equal masses of 300 g, what is the velocity of the ball two after the touch on?

A projectile of mass 2.0 kg is ﬁred in the air at an angle of 40.0

$\text{°}$

to the horizon at a speed of 50.0 m/s. At the highest point in its flight, the projectile breaks into three parts of mass 1.0 kg, 0.7 kg, and 0.three kg. The one.0-kg part falls directly down after breakup with an initial speed of 10.0 g/due south, the 0.vii-kg role moves in the original forward direction, and the 0.3-kg function goes direct up.

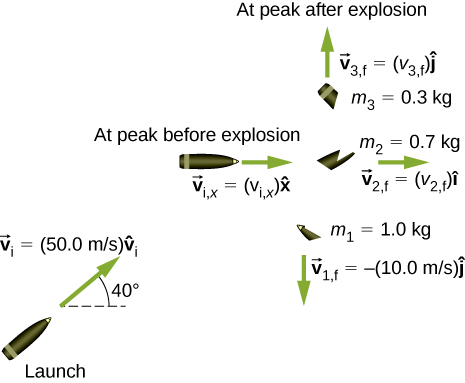
Find the speeds of the 0.3-kg and 0.7-kg pieces immediately after the break-up.
How high from the break-upward betoken does the 0.iii-kg piece go before coming to remainder?
Where does the 0.7-kg piece state relative to where it was ﬁred from?

[reveal-answer q="446915″]Show Answer[/reveal-reply]
[subconscious-answer a="446915″]a. 33 thousand/south and 110 g/s; b. 57 m; c. 480 chiliad[/hidden-answer]

Two asteroids collide and stick together. The first asteroid has mass of

$15\,×\,{10}^{3}\,\text{kg}$

and is initially moving at 770 m/due south. The second asteroid has mass of

$20\,×\,{10}^{3}\,\text{kg}$

and is moving at 1020 m/s. Their initial velocities made an angle of 20° with respect to each other. What is the final speed and direction with respect to the velocity of the first asteroid?

A 200-kg rocket in deep space moves with a velocity of

$(121\,\text{m/s})\hat{i}+(38.0\,\text{m/s})\hat{j}$

. Suddenly, it explodes into three pieces, with the first (78 kg) moving at

$\text{−}(321\,\text{m/s})\hat{i}+(228\,\text{m/s})\hat{j}$

and the second (56 kg) moving at

$(16.0\,\text{m/s})\hat{i}-(88.0\,\text{m/s})\hat{j}$

. Find the velocity of the 3rd slice.

[reveal-reply q="fs-id1167132464579″]Show Solution[/reveal-reply]

[hidden-answer a="fs-id1167132464579″]

$(732\,\text{m/s})\hat{i}+(-80.6\,\text{m/s})\hat{j}$

[/hidden-answer]

A proton traveling at

$3.0\,×\,{10}^{6}\,\text{m/s}$

scatters elastically from an initially stationary blastoff particle and is deflected at an angle of 85° with respect to its initial velocity. Given that the alpha particle has four times the mass of the proton, what pct of its initial kinetic energy does the proton retain after the collision?

Three 70-kg deer are continuing on a flat 200-kg rock that is on an ice-covered pond. A gunshot goes off and the love scatter, with deer A running at

$(15\,\text{m/s})\hat{i}+(5.0\,\text{m/s})\hat{j}$

, deer B running at

$(-12\,\text{m/s})\hat{i}+(8.0\,\text{m/s})\hat{j}$

, and deer C running at

$(1.2\,\text{m/s})\hat{i}-(18.0\,\text{m/s})\hat{j}$

. What is the velocity of the rock on which they were standing?

[reveal-answer q="fs-id1167132215564″]Testify Solution[/reveal-answer]

[hidden-answer a="fs-id1167132215564″]

$\text{−}(0.21\,\text{m/s})\hat{i}+(0.25\,\text{m/s})\hat{j}$

[/hidden-respond]

A family is skating. The father (75 kg) skates at eight.2 1000/southward and collides and sticks to the female parent (50 kg), who was initially moving at 3.3 m/s and at 45° with respect to the father's velocity. The pair then collides with their daughter (30 kg), who was stationary, and the 3 slide off together. What is their final velocity?

An oxygen cantlet (mass 16 u) moving at 733 m/southward at 15.0° with respect to the

$\hat{i}$

management collides and sticks to an oxygen molecule (mass 32 u) moving at 528 m/s at 128° with respect to the

$\hat{i}$

management. The ii stick together to class ozone. What is the final velocity of the ozone molecule?

[reveal-reply q="fs-id1167132276387″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1167132276387″]

341 thou/s at 86.viii° with respect to the

$\hat{i}$

axis.
[/subconscious-answer]

2 cars arroyo an extremely icy four-way perpendicular intersection. Motorcar A travels due north at xxx k/due south and car B is travelling e. They collide and stick together, traveling at 28° northward of east. What was the initial velocity of car B?

A 300 Car Travels at 11m/s What Is Its Momentum

9.5 Collisions in Multiple Dimensions

Learning Objectives

Problem-Solving Strategy: Conservation of Momentum in Two Dimensions

Instance

Traffic Standoff

Strategy

Significance

Check Your Understanding

Example

Exploding Scuba Tank

Strategy

Solution

Significance

Check Your Understanding

Summary

Conceptual Questions

Problems

0 Response to "A 300 Car Travels at 11m/s What Is Its Momentum"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel